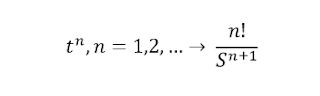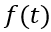UNIVERSIDAD LAICA
ELOY ALFARO DE MANABI
FACULTAD DE
INGENIERIA INDUSTRIAL
BLOG#3
TEMA: TRANSFORMADA
DE LAPLACE
AUTORES:
TANNY KIMBERLY MERA TIZON
ANDRES ALEXANDER IBARRA ZAMBRANO
JHON ALEXANDER ARANDA LOPEZ
INTRODUCCION
Con
una función:
de la cual
queremos calcular la transformada de LaPlace es igual a
pero la consideración más
sencilla que debemos observar es que los valores para resolver dentro del
camino para calcular la transformada de LaPlace es que son integrales ya
tabuladas por lo cual simplemente se evidencia la operación utilizada y se
reemplaza.
Ejemplo:
Si
tenemos una función:
buscamos en la tabla y tenemos que para esta función la
fórmula es:
entonces reemplazamos en
nuestra función quedando de la siguiente manera:
TABLA DE TRABAJO
PROPIEDADES
PRODUCTO POR UNA CONSTANTE
La
transformada de LaPlace de un producto por una constante es decir:
se resuelve de la
siguiente manera:
Ejemplo:
1.
Donde
7 es la constante y sin(8t) es la función por lo tanto procedemos a:
2.
Revisamos
en la tabla y encontramos que para el caso de sin(8t) la equivalencia es:
3.
Resultado:
LINEALIDAD
La
transformada de LaPlace en el caso que se tenga una:
es decir:
se resuelve de la
siguiente manera:
Ejemplo:
1.
Separamos
las expresiones para transformar cada una a su equivalencia:
2.
Resolvemos
individualmente con la equivalencia en la tabla:
3.
Reemplazando
en cada una tenemos:
4.
Dándonos
como resultado:
PROPIEDAD DE TRASLACION
Si
conocemos que:
podemos calcular la transformada de
como una traslación, de 
como lo
enuncia el siguiente teorema.
como lo
enuncia el siguiente teorema.
Si a es un número real y 
existe, entonces:
existe, entonces: 
Ejemplo:
Calcular la
transformada de Laplace de la siguiente función:
1. calculamos la
transformada de:
2. Resolviendo la
función en conjunto tenemos:
PROPIEDAD DE LA DERIVADA
Caso 1:
Calcular la
transformada de Laplace de la siguiente función:
1.
calculamos la transformada de f(t)
2.
Resolviendo la función en conjunto tenemos:
3. Procedemos a
derivar:
4. Remplazamos en la función en conjunto
para obtener el resultado:
Caso 2:
Calcular la
transformada de Laplace de la siguiente función:
1.
Calculamos la
transformada de la función
2.
Como se necesita la
derivada de la transformada, se calcula la segunda derivada (de acuerdo al
exponente de la función a calcular )
Primera
derivada:
Segunda
derivada:
3.
Se reemplaza en la
transformada de Laplace, pero se mantiene igual ya que el exponente es par
PROPIEDAD DE LA INTEGRAL
Ejemplo:
Calcular
la transformada de Laplace de:
1.
Se aplica el teorema de
traslación
2.
Se calcula la
transformada de la función
3.
Aplicamos la
transformada de la función de coseno y reemplazamos en la función obteniendo:
APLICACIÓN:
Una herramienta comúnmente usada en el diseño de
control clásico es la transformada de Laplace, ya que en el estudio de los
procesos es necesario considerar modelos dinámicos, es decir, modelos de
comportamiento variable respecto al tiempo, esto trae como consecuencia el uso
de ecuaciones diferenciales respecto al tiempo para representar matemáticamente
el comportamiento de un proceso.
Para poder diseñar un sistema de control automático,
se requiere:
- Conocer el proceso que se desea controlar, es decir, conocer la ecuación diferencial que describe su comportamiento, utilizando las leyes físicas, químicas o eléctricas
- A la ecuación diferencial se le llama modelo del proceso
- Una vez que se obtiene el modelo, se diseña el controlador
Ejemplo:
Obtener
la función de transferencia para el control de nivel en un tanque
Flujo que entra – Flujo que sale= acumulación
Bibliografía
FisicayMates.
(2 de Mayo de 2016). Transformada de Laplace #1 | Desde cero. Obtenido
de https://www.youtube.com/watch?v=TnXw_1RLjE0
FISICAYMATES. (s.f.). FISICAYMATES. Obtenido
de https://drive.google.com/file/d/0B9JliAFuFn_IOTR5aVZPVmNmN00/view
FisicayMates. (9 de Mayo de 2016). Transformada
de Laplace #2 | Desde cero. Obtenido de
https://www.youtube.com/watch?v=LODeBsOirJQ
